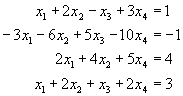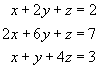| Výpočetní technika pro matematiky - DERIVE | |
| 1. seminář (22.3.2006) | |
|---|---|
|
1. Úpravy a grafické znázornění výrazů. Symbolické a grafické řešení rovnic. Rozložte výraz 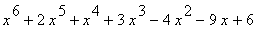 v součin činitelů v R (C). Určete nulové body výrazu a načrtněte jeho graf.
v součin činitelů v R (C). Určete nulové body výrazu a načrtněte jeho graf.
|
|
|
2. Numerické řešení rovnic. Řešte v R rovnici 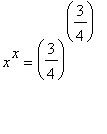 .
.
|
|
|
3. Soustavy lineárních rovnic. Úpravy matic. Rozhodněte o řešitelnosti daných soustav. Pokud řešení existuje, určete ho.
a) |
pdf
|
|
4. Soustavy lineárních rovnic. Determinant. Danou soustavu řešte užitím Cramerova pravidla: |
|
|
5. Soustavy nerovnic. Grafické a symbolické řešení. Řešte soustavy nerovnic:
a) |
|
|
6. Operace s vektory. Tvorba uživatelských funkcí. Určete vzdálenost mimoběžných přímek p, q, jsou-li určeny bodem a směrovým vektorem: p : A=[1,0,1], u =(-4,2,1); q : B=[2,1,-1], v =(-3,1,-1). |
|
| Příklady pro samostatnou práci | |
|
Algebraická rovnice. Řešte v R (C) rovnici 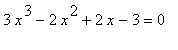 .
.
|
|
|
Transcendentní rovnice. Koza je uvázaná na provaze délky d , který je ukotven na obvodu kruhu. Určete délku d provazu tak, aby koza spásla právě polovinu plochy kruhového pozemku. Řešení znázorněte graficky. |
|
|
Programování. Napište program pro řešení kvadratické rovnice v oboru komplexních čísel. |
|
|
Užití derivace. Pro které hodnoty parametru a > 1 má rovnice 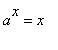 jediné řešení?
jediné řešení?
|
|
| 2. seminář (29.3.2006) | |
|
1. Limity Vypočtěte limity: a) 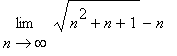 ; ;
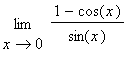 ,
c) ,
c) 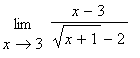 . .
|
|
|
2. Derivace funkce Vyšetřete derivaci funkce 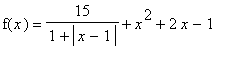 v okolí bodu x = 1.
v okolí bodu x = 1.
|
|
|
3. Průběh funkce. Vyšetřete průběh funkce dané předpisem 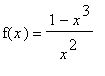 .
.
|
|
|
4. Určitý integrál. Určete objem tělesa vzniklého rotací grafu funkce |
|
|
5. Řady. Rozhodněte o konvergenci řad: a) 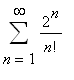 , b)
, b)
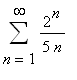 .
.
|
|
|
6. Kuželosečky. Rozhodněte, jakou kuželosečku určuje rovnice: a) 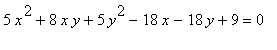 , b)
, b)
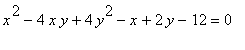 .
.
|
|
|
7. Diferenciální rovnice. U diferenciální rovnice 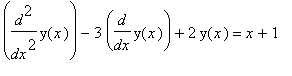 určete obecné řešení a partikulární řešení vzhledem k počátečním podmínkám
y
(0)
=
1,
y
(1)=
e
.
určete obecné řešení a partikulární řešení vzhledem k počátečním podmínkám
y
(0)
=
1,
y
(1)=
e
.
|
|
|
Zadání zápočtové práce: |
|
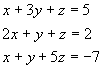 b)
b) 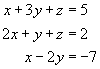 c)
c)